Abstract:
The brain processes signals of the world and transduces them into patterns of the internal code that represent these signals. Deciphering this code is the most important task of neuroscience.
To date, there are several theories of neural code. They can be classified as firing rate coding and temporal coding schemes. Anyway, all of them consider the neural activity as discrete identical spikes and just provide different versions of ‘spike train’ counting (average firing rate, spike count rate, time-dependent firing rate, temporal coding, phase of firing code, correlation coding, independent spike coding, etc.).
Some of these models contradict the realities of brain efficiency and speed. Some cover just part of the observed phenomena and fail at explaining the others. The article aims to explain these shortcomings and show a way out of the conceptual impasse that has lasted for decades. It contains an initial hypothesis about the Symphonic Neural Code that reveals the mystery of the high performance of the brain.
Keywords: neural code, signal transduction, information, brain, mind, music.
The brain is a marvel of natural information technologies evolution in terms of speed and efficiency. From this follows that of all coding schemes, the one that produces information (code patterns) more efficiently is the most likely candidate for the neural code. But do current leading theories take this obvious conclusion as a premise for their hypotheses? Let’s take a close look at the options proposed by the neuroscience mainstream.
All models consider the action potential of a neuron as the fundamental unit of the brain language. But they take it as a discrete event. From this initial assumption, they formulate the question like this: either the information is contained in the number of spikes per some time window or their exact location on the time axis. These concepts are called the rate code and the temporal code. If we take a musical analogy, this is precisely the same as if all the information would be contained in the number of notes per measure or their relative position on the time axis.
Of course, the number of notes and their sequence matter. These code parameters are there, and they are the first to catch the eye. After all, there is no information at all without notes, and sequence is part of the information. But imagine that we do not know anything about musical code and are trying to read a symphony notation. This is what neuroscientists do when they look at the recording of neuronal activity. The varying number of notes in measures and specific sequences of these notes are apparent. The central argument between the two paradigms concerns whether the timing of individual action potentials matters or we should just take the average firing rate as the varying parameter that contains the information. Some researchers believe that there are both tempo and temporal codes and translator neurons between these codes. But they all agree on one thing: action potentials are seen as similar spikes.
How can information be encoded in a stream of discrete ‘shots’? The most apparent idea comes up, and it’s almost a century old: the hypothesis that neurons transmit information to each other in the form of an average speed of spike generation. The idea was attractive by its simplicity. With all the technical complexity of spike registration, this was a feasible task even at the level of the last century’s equipment capacities. But the apparent simplicity is deceiving since the question arises about the time window over which we should average. If we analyze a monotonic signal repeating with an exact periodicity, it is not difficult for us to determine its period and calculate the average. But such an identical periodic code cannot create any information.
Proceeding from this obvious fact, the original hypothesis was based on the idea of rate variability. But if the change is not strictly periodic, then the choice of the averaging window becomes crucial. The base for averaging determines the final result. Even if we accept the hypothesis that neurons create code with their average firing rate, we must understand that neurons will calculate this average relative to the length of the cycle they know. The neuron needs to know where to start and stop adding up the number of spikes of another neuron. After all, this is the meaning of the average firing rate concept: neurons calculate the number of spikes in a certain period.
We can assume that the system clock’s presence creates the measure over which all spikes can be averaged. But then we need to define this bar. The paradox is that the task was not even set. Everyone began to measure the number of spikes relative to randomly chosen time windows (external clock with milliseconds, seconds, etc.). Moreover, arbitrary averaging algorithms were used.
Even the term ‘firing rate’ depends on the calculation procedure: the average over an arbitrary observation time or the average over several repetitions of the experiment. As a result, a tremendous amount of data has accumulated from carried out experiments over the past decades. Still, it did not bring us closer to deciphering the meaning of the code.
But suppose we somehow defined the system clock and calculated the average correctly. The question arises: what can be encoded in the average number of spikes?
Again, here comes a musical analogy. Music has a basic pulse and beat distribution that allows us to calculate the beginning and end of a measure. Suppose we have identified the bar and started calculating the average number of notes. But does it reveal the message of the music, its melodies, harmonies and rhythms? Neither the average number of notes nor the average duration of notes has any meaning. Even if we assume that all notes have the same pitch and duration (action potentials of neurons in the theory of rate coding are considered signals with the same parameters), then the rhythmic meaning of the sequences of sounds and pauses remains. Averaging simply nullifies this meaning. Any information possibly encoded in the temporal structure of the spike train is ignored in this model.
In music, the number of beats per unit of time (tempo) carries an auxiliary role. Therefore, the same piece can be played at different tempos without much change in the general meaning, and various pieces can be played at the same tempo. Averaging kills even the auxiliary meaning and tells us only how fast the musicians played on average. In addition, averaging over the population will give us not the average speed of play but the average speed of noise. But the orchestra does not make noise; it plays music, carries meanings. They are encoded in the frequency and rhythmic structure of each part and the entire piece.
There is another dead-end in this firing rate labyrinth. We cannot determine the bar if we measure the average tempo and ignore the rhythmic structure. This puts us in a paradoxical position: we need an averaging window, and we are not even concerned with defining it. We can use our arbitrary averaging windows as much as we like, even infinitely, hoping they will suddenly coincide with the system clock. This is what researchers are doing within the paradigm of the firing rate.
But even if we accidentally stumble upon the true measure of the system, we will not be able to understand it. The analysis will just give a different picture of the average rate change. But how do we determine that this is the same average at which neurons encode information for each other? Even if we measured the spikes of one neuron from pause to pause (neurons do not fire all the time), how can we determine that this is the beginning of a bar and not a pause within it?
Such is the vicious circle and the hopeless labyrinth of simple average rate analysis that neuroscience has been walking along for many years. It is, of course, not simple: many books, articles and dissertations have been written; high technologies for measuring spikes and sophisticated mathematical analysis were used. But the issue did not advance beyond the initial hypothesis. All technical dead-ends are surmountable, but the problem is that the assumption that it is possible to encode complex information in the average rate of the similar spikes is conceptually an impasse.
Now imagine that we are trying to understand musical notation by looking at the alternation of notes without considering their duration and pitch. This is what the temporal code paradigm is trying to do. Even if we think that internal characteristics of the notes do not matter and information is only in the discrete event position on the timescale, we need to know this scale to decipher the meaning. This should be an internal measure of the system, not an arbitrary chosen external clock. The problem is that spikes are not monotonous tics but a varying sequence. How can we know where the message has started or ended? How can we know what place in a message this particular spike occupies if we do not know the internal bar? Even if a neuron stops spiking, that does not mean that the message is over because the information of the temporal code is also in the pauses.
There is a further complication. The tempo of spiking varies, so each spike changes its position per external clock measure. But does it mean that the message has changed? If the internal bar remains the same but only speeds up, the message will be the same whether it is ‘played’ faster or slower. Again, a music analogy: at one tempo, the duration of notes and pauses in external units of measurement (seconds) is one, at another — different. Still, the rhythmic structure, which carries the meaning, does not change with the tempo’s variation. The durations (note values) remain the same. The whole note remains the one that sounds as long as the full bar, and the eighth note remains 1/8 of the whole. But the time of the bar can be different if the tempo changes.
The researchers try to find the reference frame for the spikes. For decades they considered the external stimulus as this frame. The logic of this linear paradigm is simple: neurons reflect stimuli, so they act in the same time frame as the external signal. So, they measured neuronal activity within the stimulation interval. The problem is that only populations that perform the initial signal transduction demonstrate time correlation with the stimulus. Neurons in the upper echelons of the chain are not aligned with it. This is natural, as neurons do not reflect signals but encode them, create signal representations. Since at a certain level of information flow in the system, the activity is more and more detached from the original signal, then at some point, it is entirely impossible to find a correlation between the spikes and the stimuli.
But even if we take the initial stage of signal transduction, the question about the time frame and what we count within it remains. The main paradigms take only spikes as carriers of information. Even if we ignore the internal characteristics of each spike and take the neural code for a digital one, we should not forget that a digital code is binary, and 1 has the same weight as 0.
Two zeros of the code are a pause twice as long as one zero. But how do we determine whether it is two zeros or one if we do not know the timescale of the system under study? This question does not bother those who think within the firing rate paradigm because it is not about rhythm (duration and sequence of activation/deactivation) but the average tempo of 1s. Within the temporal code paradigm, some voices remind everyone that 0s are essential too. Anyhow, measuring a pause against an external clock gives us a lot of data but says nothing about how many 0s there are in this particular pause.
If neurons encode information in 1s and 0s, they count them against an internal metronome. Neurons communicate in their time, normalized by the base pulse frequency. We can, of course, conduct quantitative analysis and compare the states of the system and its elements in arbitrary units of time and frequency (seconds, hertz), but this does not tell us anything about the time of the system itself. For qualitative analysis, it is necessary to normalize the system’s data according to its own time and frequencies. Then we will be able to build all our analyzes in any unit. Finding this fundamental frequency as the basis for normalization is probably of paramount importance when unraveling the brain code.
Up till now, the researchers just closed their eyes on the problem and kept generating data about spike tempo or spike sequences depending upon the paradigm they adhere to. But suppose we finally understand the meaning of the internal measure and find it out. Will it help us decipher the code if we think that it is only about discrete events and internal parameters of neural activation/deactivation do not matter? We can put the question in another way: can a code that consists of identical spikes produce the observable speed and efficiency of the brain? Do mainstream models reflect the realities of brain technology and physiology?
There is an empirical fact: the rate of change in the signal that the system manages to encode is in many cases faster than the average firing rate of neurons. A vast number of signals have dynamics measured in milliseconds, and during these milliseconds, neurons working at a speed of hundred spikes per second can only fire one or two times. With this number of spikes, it is impossible to encode the signal as an average firing rate.
The bat is capable of echolocation with a resolution of microseconds (one-millionth of a second). Based on the idea of an average firing rate code, this cannot happen just because it cannot be. But a bat does not care about our theories. It has to catch prey. As the potential prey of the bat, a moth performs complex flight paths to avoid being eaten. And its movements are controlled by neurons creating motor representations in the same time window when it is impossible to speak about any variability of the average firing rate. Even if we take relatively slow movements, they also occur within a few spikes. There is no way to encode a complex pattern with an average speed of two identical shots. Reality does not fit with the paradigm. The conclusion suggests itself: the problem is in the paradigm.
In studies within the tempo code paradigm, researchers take prolonged stimuli and, accordingly, a large number of spikes and begin to analyze the average speed. Fast stimuli of the real environment producing short spike series are simply ignored. Besides, it is assumed that different neurons encode the same information, otherwise averaging the spikes themselves and the population activity does not make any sense. But this hypothesis simply contradicts both common sense and empirical data. It is also assumed that neurons encoded the same information throughout the entire measurement of activity. But even this is not a realistic hypothesis. For example, if a spike and then a sufficiently long pause (we are talking about milliseconds) occurred, the next spike may already refer to a different sequence, to a different cycle, since the pause is part of the code. But when counting only the spikes, both fall into “one basket.” Or in a musical analogy: the notes belonged to different parts, and the pause separated them, but all the notes were piled up in the average mess because pauses in such an analysis are ignored.
There is another version of the tempo code. Why don’t neurons encode parameters with average speed relative to each other? For example, one neuron encodes a zero mark with its speed, another encodes a positive change in a signal parameter with a higher rate, and a slow one encodes a negative change. This is the so-called biased encoding. Or like this: one neuron encodes a positive change in the parameter by a proportional change in the firing rate, and the other — a negative one. Both work in shifts when the parameter changes in one direction or another (two-cell encoding). If it is necessary to encode many parameters, neurons can be combined into many pairs encoding a change in one of the signal components. Why not?
Indeed, everything is logical. But again, we run into the same physical limitations of the speed of the neurons themselves with almost instantaneous rates of signal processing and coding that they provide. This is the main stumbling block for any tempo coding scheme. It is a paradox: slow neurons work quickly. Are they ahead of themselves? This paradox is insurmountable if we look at neurons’ activity as similar spikes.
Even if we think up a virtual neuron that can shoot fast enough to encode something with an average speed, or a chain of neurons encoding a signal with relative average rates, such a code itself is so limited in information density that it cannot be a serious contender for the role of a neural code. Information about many constantly and rapidly changing parameters cannot be encoded in the tempo of identical notes. It should be contained in the note itself, in its characteristics as a wave packet with specific parameters, in combinations of notes, in sequences and durations, and pauses.
The average firing rate code is technological nonsense, as it cannot create the observable information density, speed and efficiency of the neural systems. The temporal code paradigm has a grain of truth, as information can be densely encoded in the temporal structure of activity patterns. But it still does not reflect the observable speed of the processes.
Temporal code models suggest that the information is in the exact placement of spikes and spike intervals along the timeline. In other words, it is about a binary coding system, where the spike is 1, and the pause is 0. Unlike the tempo code, with this scheme, the sequence 000111000111 means something different from 001100110011, even if the average spike rate is the same for both sequences.
The assumption that the neural code is binary and consists not only of spikes significantly increases the capacity of the code and lends credence to the theory of temporal code. But, as in the case of the average firing rate, the same question arises of correlating the code’s information capacity and the actual speed of the brain. As we have already mentioned, the brain manages to encode a complex multi-parameter signal within literally a couple of spikes. It has no time to build a long binary chain that could contain all the information.
This is where the brain is fundamentally different from artificial digital systems. For all the tremendous speed of their processors, which are orders of magnitude higher than the brain’s frequencies, they cannot match it in performance, speed and energy efficiency. The problem is that they need to process long binary codes.
The brain must use some additional capacity of the code. The environment’s signals have a complex dynamic pattern of a combination of different parameters — amplitudes, frequencies, phases. The system’s task is to create a model of these signals, which means to build a version of the original combination of many parameters. Logic dictates that the code contains information about all the parameters in a short time frame. Sometimes this window is less than the full cycle of an action potential. An obvious conclusion is that information is both in the rhythmic structure of spikes and interspike intervals and in the internal structure of the spikes themselves. Thus, complex information can be encoded in a chain of few spike/pause sequences or even within one spike.
The leading neural code models absolutely ignore this fact of life. It is a paradox: models of the neural code are not about the actual activity of neurons. There is no room for spatial-temporal nuances of a single action potential and a combination of simultaneous spikes in these models. If we use the music analogy, these models ignore the pitches of the notes, melodic, harmonic structures and polyrhythm of the mind.
The main mistake that led to the hypothesis of the neural code as modulation of the average firing rate was the logical error of mixing correlation and causality. When in 1926, researchers found a relationship between the load on a muscle and the rate of activation of motor neurons, they concluded that modulation of the firing rate is the basis of neural communication (Adrian, Zotterman, 1926). And until now, in experiments, changes in the rate of activity of neurons in different areas of the brain under various conditions of motor and cognitive activity are taken as ‘proof’ that neurons encode information in this way. The rate changes, but it can be different under various conditions, even in the same experiment with the same stimuli. And then researchers have to average even the average speed (numerous experimental attempts fall into one heap) and look for meaning in such a mess, which was not there initially, except, of course, for the only obvious thing: a change in the speed of work of a neuron. Experiments also show that neurons can produce the same average number of spikes when different stimuli are processed. It seems like this is enough to refute one of the most enduring myths in neuroscience about the tempo code, but the paradigms do not give up so easily.
The system is forced to develop fast and information-rich code to survive. It cannot do without nuances. When scientists in the laboratory calculate averages, they proceed from logic: if the basis of the code is discrete, identical pulses, then you need a sufficient statistical sample to create an average speed of such pulses. The logic is flawless, but the problem is with the initial premise that the neural code is the average number of peak phases of the oscillation, and the rest of the dynamics does not carry any information.
The approach to neurons as the creators of discrete shots with the same characteristics remains the main road of neuroscience. If the spikes are the same, then the only variable parameter is speed. The question remains about the original premise: are the spikes the same?
Moreover, the question arises: are neural action potentials spikes? It is not a weird question, though it may sound so for millions of neuroscientists used to old paradigms. A spike means a sharp point. When researchers call the activity of neurons’ spikes,’ they take them for a discrete event with no internal dynamics.
A standard recording of neuron activity looks like the same sticks, spread out with different densities along the time axis:
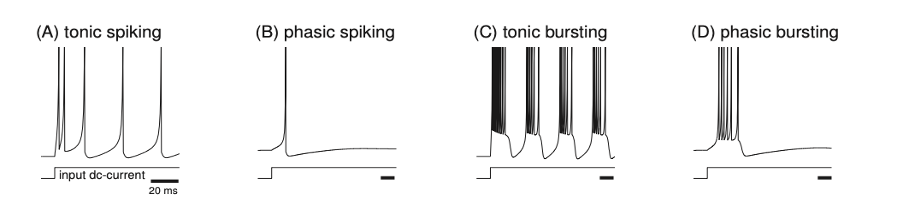
Izhikevich, 2007, www.izhikevich.com
They look like identical spikes made to the order of the firing rate coding model supporters. It remains to count the amount per unit of external time, associate it with the stimulus and understand how this stimulus is encoded in this amount. The proponents of this approach to neural code have done it for decades.
Maybe action potentials are really such even sticks? The fact of life is that they are not. It is how they are simplified in research to make them convenient for the model. And this fact is known to all involved in brain research. But it is not the first time and, probably, not the last time in science when the reality is adjusted to fit the theory instead of changing the model when it contradicts reality.
“The spike is added manually for aesthetic purposes and to fool the reader into believing that this is a spiking neuron … All spikes are implicitly assumed to be identical in size and duration … Technically, it did not fire a spike, it was only ‘said to fire a spike,’ which was added manually afterwards to fool the reader. Despite all these drawbacks, the integrate-and-fire model is an acceptable sacrifice for a mathematician who wants to prove theorems and derive analytical expressions. However, using the model might be a waste of time” (Izhikevich, 2007).
Indeed, over the decades, within the framework of this approach, thousands of scientific publications have been written, and probably hundreds of theories and models of neural code based on idealization and drawing of clear and identical spikes have been created. And all of them are not so much to “fool the reader” (although such motivation is not excluded), but more to fool themselves. It is wishful thinking: the neural code consists of the identical discrete spikes which we created ourselves, but they are so beautiful and even, and the most important thing is that we can count them and crack the neural code.
To understand whether this picture reflects reality or not, we have to go to the temporal level of the neuron itself. If we increase the resolution along the time axis, then the picture changes dramatically:
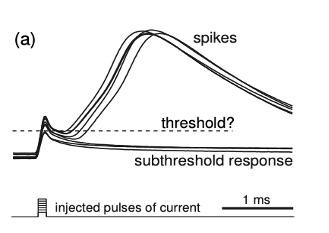
Izhikevich, 2007, www.izhikevich.com
These are in vitro recordings of the rat brain. The figure clearly shows that neurons do not fire with sharp spikes but vibrate softly with waves.
So, after decades of seeing discrete 1s where there are continuous waves, we face a question: should we continue to fool ourselves or wake up to reality? The dream was comfortable and even beneficial in gaining titles, prizes and funding. The reality is hard and even frightening. We have to change the model and experimental technologies. Probably, this road will be bumpy, but it is a lot better than drowning in the swamp of useless data and walking in conceptual circles.
For a start, we need a breakthrough in the idea about the essence of the code. Taking the music analogy again, we can formulate the following general hypothesis.
Each action potential of a neuron is a note of the music of the mind, i.e., it has individual characteristics of the waveform (period, amplitude, phase portrait), which encodes the meaning created and transmitted by the neuron to other elements of the network. Individual notes make up an activity pattern of a given neuron with a clear spatio-temporal organization making possible its integration into the general music of the mind with its melodies (frequency pattern), rhythms (phase pattern) and harmonies (simultaneous existence of different patterns). Due to this, the information density of each note (the action potential) and each pause (the resting potential) is very high, and the system as a whole has tremendous computing power, efficiency, and speed.
Here we must emphasize that musical terminology in the above hypothesis is not a metaphor but a physical analogy. The physics of the mind as a process is based on continuous oscillatory and wave phenomena. The same goes for the production of sounds that we call music.
All the complex and delicate logistics of the organization and kinetics of processes at the intracellular and intercellular level aim to create the parameters of each neuron’s oscillatory process. As a musician of an ensemble of the brain, a neuron has its instruments with specific vibrational characteristics. Its part brings meaning into the general score of a multidimensional symphony of the mind. As a result, the notes of this music can be the same and different, sound simultaneously and separately.
A fundamental paradigm shift of standard neuroscience models is required to hear and understand this music (to read the neural code). It is time to pay attention to the notes of the brain and all their characteristics: pitch, volume, duration, place in the general melodic, harmonic and rhythmic structure. Otherwise, we will not be able to write a full-fledged musical notation necessary for reading and reproducing the music of the mind.
It will not be easy since the notes of the brain are potentially infinite. But like the notes of the music of sounds, they have patterns. Identifying these patterns will allow us to read any possible piece of this music. Thus, a musician has to study the patterns of musical notation for a long time to read any piece by the score. At the moment, neuroscience, in many ways, resembles not even a beginner musician but a person who does not understand the basics of music at all. Не tries to judge it either by the number of sounds per unit of time or by a simple sequence of these sounds. Then he abandons this venture and says that there is no sense in the individual sounds and they are random, and the meaning is in general population patterns of activity. These approaches have driven us in circles and led to dead-ends for a long time.
If we take the proposed hypothesis as a working one, then we have no choice but to study the musical notation of the neural network to understand the meaning (internal characteristics) of each note, its place in the general melodic and harmonic structure (population code), rhythmic structure (temporal code), and tempo variations (firing rate). Each parameter will find its place on the musical staff of the symphony of the mind.
Why should every note be full of meaning when a code can consist of simple elements? Why are the action potentials not identical discrete spikes? They cannot be so simply because neurons are oscillators with specific parameters. They are physical systems and not ideal soldiers firing identical shots. Maybe the oscillatory nature of cells and the variety of parameters is not a disadvantage but an advantage? Thus, the information density of the neural code, even in a short interval, can be significant.
Why do many standard neuroscience theories try to represent neural code as a collection of identical digits? Of course, it’s easier to count that way. But there is one more critical point: if the model assumes ideal units of spikes, then there is no need to explain the mechanism of interaction of all these various multidimensional oscillators with many degrees of freedom. We put them into hypothetical chains and let them shoot together or alternately, but strictly with the same spikes. The only mechanism is the direct connection in the chain (synapse). It remains to express this with a mathematical model, which will take into account either simultaneity or the sequence of spikes and the strength of the connection in the chain (synaptic weight), which will determine whether neurons can fire together or not. There will be many beautiful diagrams and formulas. We can even simulate such a network on a computer and create a linear artificial neural network. And it can even do some calculations. But its effectiveness will be very far from the live network.
Real neurons will continue to be who they are: multidimensional nonlinear oscillatory systems that can receive and emit complex and multidimensional signals. They play an intricate symphony of the mind where meaning is embedded in each code element and combinations and sequences of elements. Thus, a potentially infinite set of meanings can be created from a limited set of notes. Each note (action potential) is simple enough for the code to be effective. But it also is complex enough to contain information as specific amplitude-frequency parameters and phase portrait. In this way, both the code’s high speed and informational density are achieved.
How can a neuron operating in a temporal window of milliseconds reliably encode a microsecond difference in signals? No average rate code can provide either information richness or flexibility in the required time frame. The precise placement of spikes in the internal timeline of the system and the detailing of the parameters of each spike can create meaning even within phases of a single action potential.
The number of spikes is a component of a simple level, and the parameters of the spikes themselves and their patterns are high-level components. They give the code a high degree of discriminative and generative power, i.e., increase its general informational level. But this also creates enormous difficulties when trying to decipher this code.
“Once we consider the possibility that arrival time of each spike carries information, the number of dimensions of our description increases dramatically … With an average number of spikes r ̃= 30s-1 and T ~ 300 ms, a time resolution Δt ~ 5 ms gives 2s ~ 1011 … Clearly one cannot jump from counting spikes to a ‘complete’ analysis of timing codes without some hint about how to control this explosion of possibilities” (Rieke et al., 1999).
Indeed, on the one hand, the transition to the analysis of subtle temporal nuances of neural activity leads to an explosion of possible options even in a tiny time frame of 5 milliseconds, which creates both technical and analytical difficulties. This is, of course, intimidating, and the researchers are not ready to ‘jump.’ It is much more comfortable to stay in the usual mainstream looking at the average firing rate. But this counting has been going on for almost a hundred years but did not give anything for deciphering because the code is different.
On the other hand, the explosion of analysis possibilities also creates a potential explosion of opportunities to move towards the goal, if it is about deciphering the code and not obtaining grants and titles, which are usually distributed within the framework of established paradigms.
Here we need to take an example from our neurons. “Over a time window of one second, the neuron is providing a spike which uniquely identifies one signal out of 2300 ~ 1090 possible signals” (Ibid). Such a volume is hard to imagine, but the brain simply has no other choice but to cope with a potentially endless array of signals. The neural code turned out to be not as simple as we thought because the world it encodes is not simple. The brain is complex, but this means that it can analyze itself. Our mind can crack its own code. For that, it has to create a correct model.
Suppose we accept the hypothesis that neurons encode signals of specific amplitude-frequency characteristics and phase portraits with patterns of their activity, which also have frequency and rhythmic nuances. In that case, we cannot take all spikes as equal units, average them in an arbitrary and convenient window for our measurement, average population activity, or different experiment trials. It is necessary to calculate and analyze all the subtleties of melodies, harmonies and rhythms. Technically, such a mission seems impossible at this point. But this hypothesis contains insight that gives hope for a way out of the maze. If there is a conceptual breakthrough, the technology will appear sooner or later.
“Given the evidence for performance close to the physical limits, it certainly makes sense to ask which features of neural coding and computation are essential to this remarkable performance. What is the structure of a neural code that allows such high rates of information transmission? … We would like to have a theory of the computations required to make estimates and decisions at this limiting level of reliability … Nature has built computing machinery of surprising precision and adaptability … Our story began, more or less, with Adrian’s discovery that spikes are the units out of which our perceptions must be built. We end with the idea that each of these units makes a definite and measurable contribution to those perceptions. The individual spike, so often averaged in with its neighbors, deserves more respect” (Ibid).
Yes, each note deserves more respect for two reasons: first, without it, there would be no music of the mind; second, without understanding these notes, we will not be able to read the musical notation of the neural code. Recognition of the significance of each note is a crucial step on the right path to comprehending musical notation. But the vital question about combining notes in melodies, harmonies and rhythms remains. How is the structure created? What is the nature of the code elements and the physics of the integration process? If we say that every piece of the puzzle is necessary, then the next question is equally important: how do these pieces fit together? What is the binding mechanism that allows for the code elements to preserve their individuality and combine in polyphony and polyrhythm of the symphony of the mind?
We need a theory that will be up to all these riddles that our own brain offers us. The beginning can be the formulation of hypotheses and a general concept, and then the setting of tasks for the study of these hypotheses, the creation of measurement technologies, and measurement analysis. First comes the model; practice follows. If the model is correct, practice will move in the direction of light. If the model is wrong, practice will walk in the dark. We should just correct the model. Easier said than done, as the models tend to ‘stick to their guns.’ But the road is made by walking.
The Teleological Transduction Theory (TTT) tries to show the light at the end of the tunnel by proposing a physically and technologically grounded model of the mind (Tregub, 2021). One of the hypotheses within its framework is the assumption that neural code is analogous to musical code. A fundamental change in the paradigm is the idea that the action potentials are not identical units but the notes of the music of the mind with internal characteristics. These notes carry information in the waveform of each action potential. Thus, a series of notes becomes a melody, and simultaneous combinations of a vast number of notes become chords and harmonies of the mind. We can call it a Symphonic Neural Code hypothesis.
This simple hypothesis leads to a conclusion that cannot be called trivial for two reasons. First, it contradicts mainstream neuroscience theories and requires a paradigm shift. Second, it leads to complex conceptual and technological consequences for the experimental research process.
We will have to change the neural network study’s approaches and technologies. One thing is to count the number of spikes per unit of time. It is quite another thing to get information about the parameters of each action potential, about its place in the general pattern of activity and silence (neurons are silent as meaningfully as they speak). It is one thing to average a population’s activity, throw out what seems like noise from it, and exclude pauses altogether. Another thing is to hear all the melodic and rhythmic moves, all the harmonic combinations in the general choir. The study of spatiotemporal patterns’ details requires state-of-the-art recording techniques. Present equipment does not yet allow us to write a full-fledged musical notation of the music of the Mind. But our models should move technologies forward, not trail behind.
Stanislav Tregub
References:
- Adrian, ED, Zotterman, Y. (1926). The impulses produced by sensory nerve endings: Part II: The response of a single end organ. J Physiol (Lond.). 61: 151–171.
- Izhikevich, E. M. (2007). Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting . The MIT Press, Cambridge, MA .
- Rieke, F., Bialek, W., Warland, D., de Ruyter van Steveninck, R. R. (1999). Spikes: Exploring the neural code. MIT Press, Cambridge.
- Tregub, S. (2021). Symphony of Matter and Mind. Part 1,2,3,4,5,6,7,8. https://stanislavtregub.com/
DOI: 10.13140/RG.2.2.35426.25289